判断点与多边形的关系
射线法
算法原理
从待判断点向某一方向引射线,计算与多边形交点的个数,如果是偶数或者0,则点在多边形外;如果是奇数,则点在多边形内。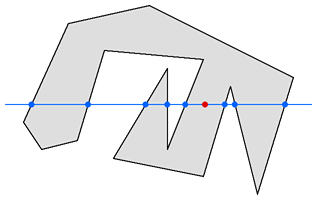
特殊情况
1.点在多边形上
2.点与多边形顶点重合
3.射线经过多边形顶点
4.射线刚好经过多边形的一条边
解决方案
1.判断点在线上,如计算点与两个端点连线斜率是否相等
2.点和多边形重合,比较坐标
3.顶点穿越问题。
面积法
1 算法原理
如果点在多边形内部或者边上,那么点与多边形所有边组成的三角形面积和等于多边形面积。多边形的面积公式可以用差积计算。
转角法
1 算法原理
按照多边形定点逆时针顺序,从P点到定点Vi分别连线,其中αi为Vi和Vi+1之间的夹角。如果α家督逆时针为正,顺时针为负,这样到所有顶点做连线之间夹角和为0,则点P在多边形内,否贼在外。
弧长法
1 算法原理
弧长法是改进后的转角法,解决了传统转角法的精度问题。算法思想是,以被测点O为坐标原点,将平面划分为4个象限,对每个多边形顶点P[i],计算其所在的象限,然后顺序访问多边形的各个顶点P[i],分析P[i]和P[i+1],有下列三种情况:
(1)P[i+1]在P[i]的下一象限。此时弧长和加π/2;
(2)P[i+1]在P[i]的上一象限。此时弧长和减π/2;
(3)P[i+1]在Pi的相对象限。利用叉积f=y[i+1]x[i]-x[i+1]y[i]计算Op[i]与Op[i+1]的关系,若f=0,Op[i]与Op[i+1]共线,点在多边形边上;若f<0,Op[i+1]在Op[i]逆时针方向,弧长和减π;若f>0,Op[i+1]在Op[i]顺时针方向,弧长和加π。
由于顶点在原点和坐标轴上时需要特殊处理,为了准确性,应该在每次计算顶点时都用叉积判断P是否在当前边上,另外将π用整数代替可以避免浮点数的精度误差。