自编码网络 - 墨缘晓生

自编码网络介绍及应用

自编码网络是非监督学习领域中的一种，可以自动从无标注的数据中学习特征，是一种以重构输入信号为目标的神经网络，可以给出比原始数据更好的特征描述，具有较强的特征学习能力。

醉简单的自编码网络

自编码（Auto-Encoder，AE）网络是输入等于输出的网络，最基本的模型可以视为三层的神经网络，即输入层、隐藏层、输出层。其中，输入层的样本也会充当输出层的标签角色。换句话说，这个神经网络就是一种尽可能复现输入信号的神经网络。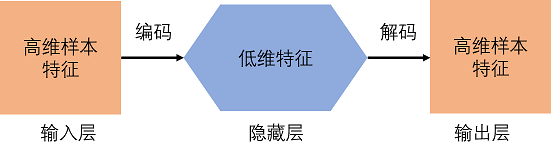
让输出信号等于输入信号

其中从输入到中间状态的过程叫编码，从中间状态再回到输出的过程叫解码，这样构成的自动编码器可以捕捉代表输入数据最重要的因素，类似于PCA，找到可以代表原信息的主要成分。
自编码器要求输出尽可能等于输入，并且其隐藏层必须满足一定的稀疏性，是通过将影藏层中的后一层个数比前一层神经元个数少的方式来实现稀疏效果。相当于隐藏层对输入进行了压缩，并在输出层中解压缩。整个过程中肯定会丢失信息，但训练能够使丢失的信息尽量减少，最大化的保留其主要特征。如果激活函数不使用Sigmoid函数，而使用线性函数，那么便是PCA模型了。

自编码网络的代码实现

提取图片特征并利用特征还原图片

通过构建一个两层降维的自编码网络，将MNIST数据集的数据特征提取出来，并通过这些特征再重建一个MNIST数据集。
下面输入MNIST数据集的图片，将其像素点组成的数据（28x28=784）从784维降维到256，再降到128，最后再以同样的方式经过128再经过256，最终还原到原来的图片。过程如下图所示。
自编码实例代码的维度变化过程

import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
from tensorflow.examples.tutorials.mnist import input_data
mnist = input_data.read_data_sets("../MNIST_data/", one_hot=True)
# 定义模型
learning_rate = 0.01
n_hidden_1 = 256  # 第一层256个节点
n_hidden_2 = 128  # 第二层128个节点
n_input = 784  # MNIST数据集中图片的维度

x = tf.placeholder("float", [None, n_input])
y = x
# 学习参数
weights = {
    'encoder_h1': tf.Variable(tf.random_normal([n_input, n_hidden_1])),
    'encoder_h2': tf.Variable(tf.random_normal([n_hidden_1, n_hidden_2])),
    'decoder_h1': tf.Variable(tf.random_normal([n_hidden_2, n_hidden_1])),
    'decoder_h2': tf.Variable(tf.random_normal([n_hidden_1, n_input]))
}
biases = {
    'encoder_b1': tf.Variable(tf.zeros([n_hidden_1])),
    'encoder_b2': tf.Variable(tf.zeros([n_hidden_2])),
    'decoder_b1': tf.Variable(tf.zeros([n_hidden_1])),
    'decoder_b2': tf.Variable(tf.zeros([n_input]))
}


# 编码
def encoder(x):
    layer_1 = tf.nn.sigmoid(
        tf.add(tf.matmul(x, weights['encoder_h1']), biases['encoder_b1']))
    layer_2 = tf.nn.sigmoid(
        tf.add(
            tf.matmul(layer_1, weights['encoder_h2']), biases['encoder_b2']))
    return layer_2


# 解码
def decoder(x):
    layer_1 = tf.nn.sigmoid(
        tf.add(tf.matmul(x, weights['decoder_h1']), biases['decoder_b1']))
    layer_2 = tf.nn.sigmoid(
        tf.add(
            tf.matmul(layer_1, weights['decoder_h2']), biases['decoder_b2']))
    return layer_2


# 输出节点
encoder_out = encoder(x)
pred = decoder(encoder_out)
# cost为有与pred的平方差
cost = tf.reduce_mean(tf.pow(y - pred, 2))
optimizer = tf.train.RMSPropOptimizer(learning_rate).minimize(cost)
# 由于输出标签也是输入标签,所以后面直接定义y=x
# 开始训练
training_epochs = 20  # 一共迭代20次
batch_size = 256  # 每次取256个样本
display_step = 5  # 迭代5次输出一次信息
with tf.Session() as sess:
    sess.run(tf.global_variables_initializer())
    total_batch = int(mnist.train.num_examples / batch_size)
    # 开始训练
    for epoch in range(training_epochs):
        for i in range(total_batch):
            batch_xs, batch_ys = mnist.train.next_batch(batch_size)  # 取数据
            _, c = sess.run([optimizer, cost], feed_dict={x: batch_xs})
            # 训练模型
        if epoch % display_step == 0:
            print("Epoch:", "%04d" % (epoch + 1), "cost=", "{:.9f}".format(c))
    print("完成")
    # 测试模型
    correct_predicition = tf.equal(tf.argmax(pred, 1), tf.argmax(y, 1))
    # 计算错误率
    accuracy = tf.reduce_mean(tf.cast(correct_predicition, "float"))
    print("accuracy:", 1 - accuracy.eval({
        x: mnist.test.images,
        y: mnist.test.images
    }))

    # 随意取出10张图片,对比输入和输出
    show_num = 10
    reconstruction = sess.run(
        pred, feed_dict={x: mnist.test.images[:show_num]})
    f, a = plt.subplots(2, 10, figsize=(10, 2))
    for i in range(show_num):
        a[0][i].imshow(np.reshape(mnist.test.images[i], (28, 28)))
        a[1][i].imshow(np.reshape(reconstruction[i], (28, 28)))
    plt.show()

图片分为上下两行，第一行显示的是输入图片，第二行显示的输出图片。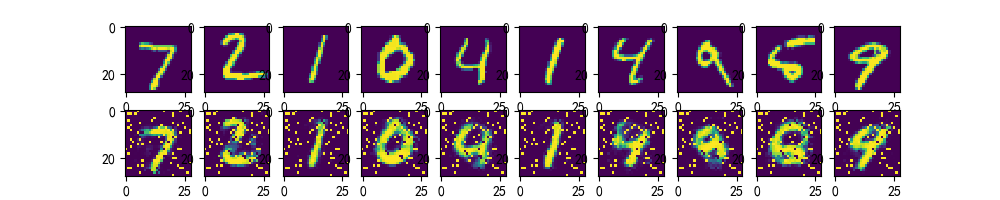
自编码实例输出结果

线性解码器

上例中使用的激活函数输出范围是[0,1]，当对最终提取的特征节点采用该激励函数时，就相当于对输入限制或缩放，是其位于[0,1]范围中，有些数据集如MNIST能方便的将输出缩放到[0,1]中，但是很难满足对输入值的要求。例，PCA白化处理的输入并不满足[0,1]范围要求。
如果你用一个恒等式来作为激励函数，就可以解决这个问题，即将f(z)=z作为激励函数，即没有激励函数。

这个方法只是对最后的输出层而言，对于神经网络中隐含的神经元依然还要使用S型或其他激活函数。

由多个带有S型激活函数的隐含层及一个线性输出层构成的自编码器，称为线性解码器。

提取图片的二位特征，并利用二维特征还原图片

在自编码网络中使用线性解码器对MNIST数据特征进行再压缩，并将其映射到直角坐标系上。这里使用4层逐渐压缩将784维分别压缩成256、64、16、2这4个特征向量。
线性解码器部分网络结构

然后以直角坐标系的形式将数据点显示出来，这样可以更直观的看到自编码器对于同一类图片的聚类效果。

如果想得到更好的特征提取效果，可以将压缩的层数变得更多，（如512、256、128、64、32、16、2），由于Sigmoid函数天生缺陷，无法使用更深的层，所以这里只能做成4层。

import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
from tensorflow.examples.tutorials.mnist import input_data
mnist = input_data.read_data_sets("../MNIST_data/", one_hot=True)
learning_rate = 0.01
n_hidden_1 = 256  # 第一层256个节点
n_hidden_2 = 64
n_hidden_3 = 16
n_hidden_4 = 2
n_input = 784  # MNIST数据集中图片的维度
x = tf.placeholder("float", [None, n_input])
y = x
# 学习参数
weights = {
    'encoder_h1': tf.Variable(tf.random_normal([n_input, n_hidden_1])),
    'encoder_h2': tf.Variable(tf.random_normal([n_hidden_1, n_hidden_2])),
    'encoder_h3': tf.Variable(tf.random_normal([n_hidden_2, n_hidden_3])),
    'encoder_h4': tf.Variable(tf.random_normal([n_hidden_3, n_hidden_4])),
    'decoder_h1': tf.Variable(tf.random_normal([n_hidden_4, n_hidden_3])),
    'decoder_h2': tf.Variable(tf.random_normal([n_hidden_3, n_hidden_2])),
    'decoder_h3': tf.Variable(tf.random_normal([n_hidden_2, n_hidden_1])),
    'decoder_h4': tf.Variable(tf.random_normal([n_hidden_1, n_input]))
}
biases = {
    'encoder_b1': tf.Variable(tf.zeros([n_hidden_1])),
    'encoder_b2': tf.Variable(tf.zeros([n_hidden_2])),
    'encoder_b3': tf.Variable(tf.zeros([n_hidden_3])),
    'encoder_b4': tf.Variable(tf.zeros([n_hidden_4])),
    'decoder_b1': tf.Variable(tf.zeros([n_hidden_3])),
    'decoder_b2': tf.Variable(tf.zeros([n_hidden_2])),
    'decoder_b3': tf.Variable(tf.zeros([n_hidden_1])),
    'decoder_b4': tf.Variable(tf.zeros([n_input]))
}
'''
定义网络模型
在编码的最后一层,没有进行sigmoid变换,是因为生成的二维数据其数据特征已经变得极为重要,
所以希望让它透传到解码器中,少一些变换可以最大化的保留原有的主要特征
'''
def encoder(x):
    layer_1 = tf.nn.sigmoid(
        tf.add(tf.matmul(x, weights['encoder_h1']), biases['encoder_b1']))
    layer_2 = tf.nn.sigmoid(
        tf.add(
            tf.matmul(layer_1, weights['encoder_h2']), biases['encoder_b2']))
    layer_3 = tf.nn.sigmoid(
        tf.add(
            tf.matmul(layer_2, weights['encoder_h3']), biases['encoder_b3']))
    layer_4 = tf.add(
        tf.matmul(layer_3, weights['encoder_h4']), biases['encoder_b4'])
    return layer_4
def decoder(x):
    layer_1 = tf.nn.sigmoid(
        tf.add(tf.matmul(x, weights['decoder_h1']), biases['decoder_b1']))
    layer_2 = tf.nn.sigmoid(
        tf.add(
            tf.matmul(layer_1, weights['decoder_h2']), biases['decoder_b2']))
    layer_3 = tf.nn.sigmoid(
        tf.add(
            tf.matmul(layer_2, weights['decoder_h3']), biases['decoder_b3']))
    layer_4 = tf.nn.sigmoid(
        tf.add(
            tf.matmul(layer_3, weights['decoder_h4']), biases['decoder_b4']))
    return layer_4
enocder_op = encoder(x)
y_pred = decoder(enocder_op)
cost = tf.reduce_mean(tf.square(y - y_pred))  # 均方误差损失函数
# cost = tf.reduce_mean(tf.pow(y - y_pred, 2))
optimizer = tf.train.AdamOptimizer(learning_rate).minimize(cost)
training_epochs = 20
batch_size = 256
# display_step = 1
with tf.Session() as sess:
    sess.run(tf.global_variables_initializer())
    total_batch = int(mnist.train.num_examples / batch_size)
    for epoch in range(training_epochs):
        for i in range(total_batch):
            batch_xs, batch_ys = mnist.train.next_batch(batch_size)
            _, c = sess.run([optimizer, cost], feed_dict={x: batch_xs})
        print("Epoch:", '%04d' % (epoch + 1), 'cost=', '{:.9f}'.format(c))
    print('完成')
    show_num = 10
    encode_decode = sess.run(
        y_pred, feed_dict={x: mnist.test.images[:show_num]})
    f, a = plt.subplots(2, 10, figsize=(10, 2))
    for i in range(show_num):
        a[0][i].imshow(np.reshape(mnist.test.images[i], (28, 28)))
        a[1][i].imshow(np.reshape(encode_decode[i], (28, 28)))
    plt.show()
    # 显示数据的二维特征
    a = [np.argmax(1) for l in mnist.test.labels]  # 将one_hot转成一般编码
    encoder_result = sess.run(enocder_op, feed_dict={x: mnist.test.images})
    plt.scatter(encoder_result[:, 0], encoder_result[:, 1], c=a)
    plt.colorbar()
    plt.show()

实现卷积网络的自编码

import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
from tensorflow.examples.tutorials.mnist import input_data
mnist = input_data.read_data_sets("../MNIST_data/", one_hot=True)


# 最大池化
def max_pool_with_argmax(net, stride):
    _, mask = tf.nn.max_pool_with_argmax(
        net,
        ksize=[1, stride, stride, 1],
        strides=[1, stride, stride, 1],
        padding='SAME')
    mask = tf.stop_gradient(mask)
    net = tf.nn.max_pool(
        net,
        ksize=[1, stride, stride, 1],
        strides=[1, stride, stride, 1],
        padding='SAME')
    return net, mask


# 4*4----2*2--=2*2 [6,8,12,16]
# 反池化
def unpool(net, mask, stride):
    ksize = [1, stride, stride, 1]
    input_shape = net.get_shape().as_list()

    output_shape = (input_shape[0], input_shape[1] * ksize[1],
                    input_shape[2] * ksize[2], input_shape[3])

    one_like_mask = tf.ones_like(mask)
    batch_range = tf.reshape(
        tf.range(output_shape[0], dtype=tf.int64),
        shape=[input_shape[0], 1, 1, 1])
    b = one_like_mask * batch_range
    y = mask // (output_shape[2] * output_shape[3])
    x = mask % (output_shape[2] * output_shape[3]) // output_shape[3]
    feature_range = tf.range(output_shape[3], dtype=tf.int64)
    f = one_like_mask * feature_range

    updates_size = tf.size(net)
    indices = tf.transpose(
        tf.reshape(tf.stack([b, y, x, f]), [4, updates_size]))
    values = tf.reshape(net, [updates_size])
    ret = tf.scatter_nd(indices, values, output_shape)
    return ret


def conv2d(x, W):
    return tf.nn.conv2d(x, W, strides=[1, 1, 1, 1], padding='SAME')


def max_pool_2x2(x):
    return tf.nn.max_pool(
        x, ksize=[1, 2, 2, 1], strides=[1, 2, 2, 1], padding='SAME')


def encoder(x):
    h_conv1 = tf.nn.relu(
        tf.add(conv2d(x, weights['encoder_conv1']), biases['encoder_conv1']))
    h_conv2 = tf.nn.relu(
        tf.add(
            conv2d(h_conv1, weights['encoder_conv2']),
            biases['encoder_conv2']))
    return h_conv2, h_conv1


def decoder(x, conv1):
    t_conv1 = tf.nn.conv2d_transpose(x - biases['decoder_conv2'],
                                     weights['decoder_conv2'], conv1.shape,
                                     [1, 1, 1, 1])
    t_x_image = tf.nn.conv2d_transpose(t_conv1 - biases['decoder_conv1'],
                                       weights['decoder_conv1'], x_image.shape,
                                       [1, 1, 1, 1])
    return t_x_image


# 网络模型参数
learning_rate = 0.01
n_conv_1 = 16
n_conv_2 = 32
n_input = 784
batchsize = 50
x = tf.placeholder('float', [batchsize, n_input])
x_image = tf.reshape(x, [-1, 28, 28, 1])
# 学习参数
weights = {
    'encoder_conv1':
    tf.Variable(tf.truncated_normal([5, 5, 1, n_conv_1], stddev=0.1)),
    'encoder_conv2':
    tf.Variable(tf.random_normal([3, 3, n_conv_1, n_conv_2], stddev=0.1)),
    'decoder_conv1':
    tf.Variable(tf.random_normal([5, 5, 1, n_conv_1], stddev=0.1)),
    'decoder_conv2':
    tf.Variable(tf.random_normal([3, 3, n_conv_1, n_conv_2], stddev=0.1))
}
biases = {
    'encoder_conv1': tf.Variable(tf.zeros([n_conv_1])),
    'encoder_conv2': tf.Variable(tf.zeros([n_conv_2])),
    'decoder_conv1': tf.Variable(tf.zeros([n_conv_1])),
    'decoder_conv2': tf.Variable(tf.zeros([n_conv_2])),
}

#输出的节点
encoder_out, conv1 = encoder(x_image)
h_pool2, mask = max_pool_with_argmax(encoder_out, 2)

h_upool = unpool(h_pool2, mask, 2)
pred = decoder(h_upool, conv1)
# 使用平方差为cost
cost = tf.reduce_mean(tf.pow(x_image - pred, 2))
optimizer = tf.train.RMSPropOptimizer(learning_rate).minimize(cost)

# 训练参数
training_epochs = 20  #一共迭代20次

display_step = 5  #迭代5次输出一次信息

# 启动绘话
with tf.Session() as sess:
    sess.run(tf.global_variables_initializer())
    total_batch = int(mnist.train.num_examples / batchsize)
    # 开始训练
    for epoch in range(training_epochs):  #迭代
        for i in range(total_batch):
            batch_xs, batch_ys = mnist.train.next_batch(batchsize)  #取数据
            _, c = sess.run([optimizer, cost], feed_dict={x: batch_xs})  # 训练模型
        if epoch % display_step == 0:  # 现实日志信息
            print("Epoch:", '%04d' % (epoch + 1), "cost=", "{:.9f}".format(c))
    print("完成")
    # 测试
    batch_xs, batch_ys = mnist.train.next_batch(batchsize)
    # print("Error:", cost.eval({x: batch_xs}))
    show_num = 10
    reconstruction = sess.run(
        #pred, feed_dict={x: mnist.test.images[:show_num]})
        pred,
        feed_dict={x: batch_xs})
    f, a = plt.subplots(2, 10, figsize=(10, 2))
    for i in range(show_num):
        #a[0][i].imshow(np.reshape(mnist.test.images[i], (28, 28)))
        a[0][i].imshow(np.reshape(batch_xs[i], (28, 28)))
        a[1][i].imshow(np.reshape(reconstruction[i], (28, 28)))
    plt.show()

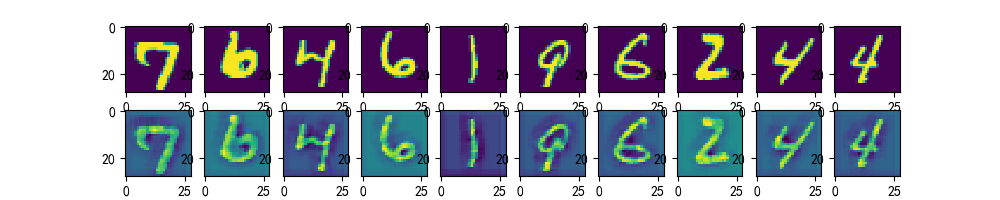
去噪自编码

去噪自动编码器（Denoising Autoencoder，DA），在自动编码的基础上，训练数据加入噪声，输出的标签仍是原始的样本（没有加噪声），这样自动编码器必须学习去除噪声而获得真正没有被噪声污染过的输入特征。
在实际训练中，人为加入噪声有两种方式：
1）在选择训练数据集时，额外选择一些样本集以外的数据。
2）改变已有的样本数据集中的数据（使样本个体不完整，或通过噪声与样本进行的加减乘除之类的运算，使样本数据发生变化）

import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
from tensorflow.examples.tutorials.mnist import input_data
mnist = input_data.read_data_sets("../MNIST_data/", one_hot=True)
train_X = mnist.train.images
train_Y = mnist.train.labels
test_X = mnist.test.images
test_Y = mnist.test.labels
n_input = 784
n_hidden_1 = 256
x = tf.placeholder('float', [None, n_input])
y = tf.placeholder('float', [None, n_input])
dropout_keep_prob = tf.placeholder('float')
weights = {
    'h1': tf.Variable(tf.random_normal([n_input, n_hidden_1])),
    'h2': tf.Variable(tf.random_normal([n_hidden_1, n_hidden_1])),
    'out': tf.Variable(tf.random_normal([n_hidden_1, n_input]))
}
biases = {
    'b1': tf.Variable(tf.zeros([n_hidden_1])),
    'b2': tf.Variable(tf.zeros([n_hidden_1])),
    'out': tf.Variable(tf.zeros([n_input]))
}


# 网络模型
def denoise_auto_encoder(x, weights, biases, keep_prob):
    layer_1 = tf.nn.sigmoid(tf.add(tf.matmul(x, weights['h1']), biases['b1']))
    layer_1out = tf.nn.dropout(layer_1, keep_prob)
    layer_2 = tf.nn.sigmoid(
        tf.add(tf.matmul(layer_1out, weights['h2']), biases['b2']))
    layer_2out = tf.nn.dropout(layer_2, keep_prob)
    return tf.nn.sigmoid(
        tf.add(tf.matmul(layer_2out, weights['out']), biases['out']))


reconstruction = denoise_auto_encoder(x, weights, biases, dropout_keep_prob)

# cost计算
cost = tf.reduce_mean(tf.pow(reconstruction - y, 2))
optm = tf.train.AdamOptimizer(0.01).minimize(cost)
# 训练参数
epochs = 20
batch_size = 256
disp_step = 2
with tf.Session() as sess:
    sess.run(tf.global_variables_initializer())
    print('开始训练')
    for epoch in range(epochs):
        num_batch = int(mnist.train.num_examples / batch_size)
        total_cost = 0
        for i in range(num_batch):
            batch_xs, batch_ys = mnist.train.next_batch(batch_size)
            batch_xs_noisy = batch_xs + 0.3 * np.random.randn(batch_size, 784)
            feeds = {x: batch_xs_noisy, y: batch_xs, dropout_keep_prob: 1.}
            sess.run(optm, feed_dict=feeds)
            total_cost += sess.run(cost, feed_dict=feeds)
        if epoch % disp_step == 0:
            print("Epoch %02d/%02d average cost:%.6f" %
                  (epoch, epochs, total_cost / num_batch))
    print('完成')
    show_num = 10
    test_noisy = mnist.test.images[:show_num] + 0.3 * np.random.randn(
        show_num, 784)
    encode_decode = sess.run(
        reconstruction, feed_dict={
            x: test_noisy,
            dropout_keep_prob: 1.
        })
    f, a = plt.subplots(3, 10, figsize=(10, 3))
    for i in range(show_num):
        a[0][i].imshow(np.reshape(test_noisy[i], (28, 28)))
        a[1][i].imshow(np.reshape(mnist.test.images[i], (28, 28)))
        a[2][i].matshow(
            np.reshape(encode_decode[i], (28, 28)), cmap=plt.get_cmap('gray'))
    plt.show()

    # 测试鲁棒性
    randidx = np.random.randint(test_X.shape[0], size=1)
    orgvec = test_X[randidx, :]
    testvec = test_X[randidx, :]
    label = np.argmax(test_Y[randidx, :], 1)
    print('label is %d' % label)
    # 噪声类型
    print('Salt and Pepper Noise')
    noisyvec = testvec
    rate = 0.15
    noiseidx = np.random.randint(
        test_X.shape[1], size=int(test_X.shape[1] * rate))
    noisyvec[0, noiseidx] = 1 - noisyvec[0, noiseidx]
    outvec = sess.run(
        reconstruction, feed_dict={
            x: noisyvec,
            dropout_keep_prob: 1
        })
    outimg = np.reshape(outvec, (28, 28))

    plt.matshow(np.reshape(orgvec, (28, 28)), cmap=plt.get_cmap('gray'))
    plt.title('Original Image')
    plt.colorbar()

    plt.matshow(np.reshape(noisyvec, (28, 28)), cmap=plt.get_cmap('gray'))
    plt.title('Input Image')
    plt.colorbar()

    plt.matshow(outimg, cmap=plt.get_cmap('gray'))
    plt.title('Reconstructed Image')
    plt.colorbar()
    plt.show()

栈式自编码

栈式自编码介绍

栈式自编码神经网络（Stacked Autoencoder，SA），是对自编码网络的一种使用方法，是一个由多层训练好的自编码器组成的神经网络。由于网络中的每一层都是单独训练而来，相当于都初始化了一个合理的数值。所以，这样的网络会更容易训练，并且有更快的收敛性及更高的准确度。栈式自编码常被用于预训练（初始化）深度神经网络之前的权重预训练步骤。例如，在一个分类问题上，可以按照从前向后的顺序执行每一层通过自编码器来训练，最终将网络中最深层输出作为softmax分类器的输入特征，通过softmax层将其分开。
下面以训练一个包含两个隐含层的栈式自编码网络为例。
1)训练一个自编码器，得到原始输入的一阶特征表示h⁽¹⁾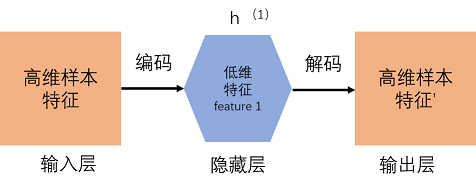
栈式自编码一层结构
2)将上一步输出的特征h⁽¹⁾作为输入，对其进行再一次的自编码，并同时获取特征h⁽²⁾.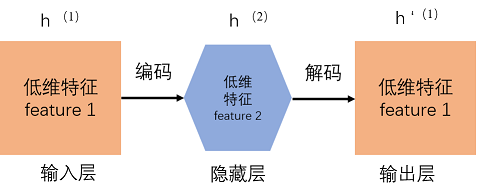
栈式自编码二层结构
3)把上一步的特征h⁽²⁾连还是哪个softmax分类器，得到了一个图片数字标签分类的模型，结构如下图所示。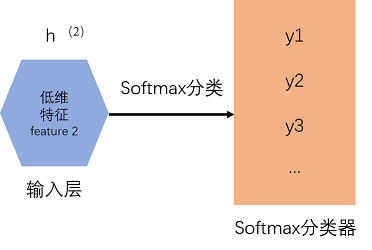
栈式自编码三层结构
4)把这3层结合起来，就构成一个包含两个隐藏层加一个softmax的栈式自编码网络，可以对数字图片分类。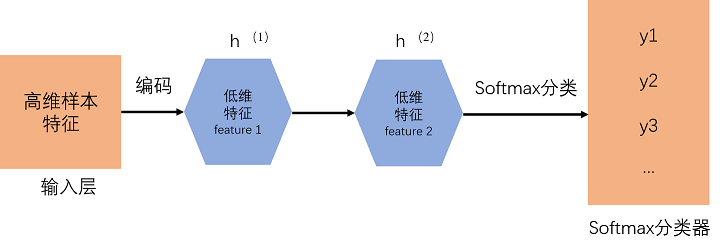
栈式自编码级联结构

栈式自编码在深度学习中的意义

优点：

每一层都可以单独训练，保证将维特征的可控性
使用栈式自编码逐层降维，可以将复杂问题简单化。
任意深层，理论上是越深层的神经网络对现实的拟合度越高，但是传统的多层神经网络，由于使用的是误差反向传播方式，导致层越深，传播的误差越小。栈式自编码巧妙地绕过这个问题，直接使用降维后的特征值进行二次训练，可以任意层数的加深。

栈式自编码通常能够获取到输入的“层次型分组”或“部分-整体分解”结构，自编码器倾向于学习得到与样本相对应的低维向量，该向量可以更好地表示高维样本的数据特征。
如果网络的输入是图像，第一层会学习去识别边，二层会学习组合边、构成轮廓角等，更高层会学习组合更形象的特征。

文章目录